Malaysia ACM ICPC 2018 Solution Writeup
I participated in this contest as my final national ACM-ICPC contest. With a certain amount of luck, my teammates (Jenn Pang and Wing Khang) and I won the contest.
The contest is held on 11th & 12th May 2018 at International Islamic University Malaysia (IIUM), Kuala Lumpur. It consists of 10 problems to be solved in 5 hours.
Before the contest, we have developed a few strategies including separate the task of reading and understanding problem statement equally to all 3 members in our team. Also, not to forgot that the rule of thumb of doing the contest is that we should always solve the problems in the sequence of difficulty, easy to hard (or I should say, in the sequence of confidence level, from high to low). Lastly, we know that we should always observe the scoreboard and solve the problem that many people had solved.
Following are my post-contest solution write-up of the competition together with some in-contest thought and situation. All the AC codes are available at here.
Note: All the variables below are referring to the problem statement, if not defined explicitly.
Some Opinion on the Contest
This year, the problems have generally higher quality than every previous year contest, thanks to the problem setters this year. There are still room to improve but at least, weird problem, confusing statement, and super low quality test data do not exist.
It is great to see such improvements in my national ACM-ICPC contest. Hope that the contest quality can continue to improve in following years.
A - Aku Negaraku
This is the second problem our team solved. Jenn Pang has understood the problem and decide to implement it. I helped a bit in the debugging of the indexing problem and we get AC after that.
Solution: Ad-Hoc - Simulation (Code)
This is a simulation problem. After doing complexity analysis, naive simulation of the process is \(O(n^2m)\) which is feasible. The naive implementation is described as below:
Use a boolean array to keep track of whether person \(i\) has been kicked or not. Loop \(n-1\) times where each iteration will kick \(1\) person. For each iteration, to find the next person to kick we simply iterate through the array, one by one, skip those who has been kicked in the previous iterations. The following shows 2 methods of implementing this simulation.
Implementation 1
int cur = 0; // use a index to keep track of current position
// outer loop, n-1 times, each time kick 1 person
for(int i = 0; i < n-1; i++){
// inner loop, to skip m times
for(int j = 0; j < m; j++){
cur++; if(cur == n+1) cur = 1; // n -> 1 -> 2 -> ...
if(selected[cur])
j--; // this person had been kicked, we should not advance the j counter
}
// after skipped m times, cur is the next person to kick
selected[cur] = true; // kick this person
}
// output idx where selected[idx] == false
Implementation 2
int cur = -1; // use a index to keep track of current position
// outer loop, n-1 times, each time kick 1 person
for(int i = 0; i < n-1; i++){
// inner loop, to skip m times
for(int j = 0; j < m; j++){
cur = (cur+1)%n; // n-1 -> 0 -> 1 -> ...
while(selected[cur])
cur = (cur+1)%n;
}
// after skipped m times, cur is the next person to kick
selected[cur] = true; // kick this person
}
// output idx+1 where selected[idx] == false
The second implementation uses \(0\)-based indexing to enable the use of modulus, cur = (cur+1)%n; and use while loop to find the next available person.
B - Cheap Deliveries
Immediately after I understand this problem, I notice that it is a TSP (Travelling Salesman Problem) with DP problem. However, because of the implementation difficulties and uncertainty, we actually left this problem behind and solve other problem first.
Solution: Graph - TSP with DP (Code)
Variable declaration. Let
- \(k\) be the number of item to be delivered, given \(k \le 18\)
- \(u_i\) be the pickup location of the \(i\)-th item
- \(v_i\) be the dropoff location of the \(i\)-th item
The key to identifies this as a TSP are:
- Abu must deliver all \(k\) items
- Abu can choose any other items as his next items to deliver
- It seeks for minimum total travel distance
However, after identifying this as a TSP, we still need a few observations and pre-processing to solve this problem. We need to observe that:
- Since all \(k\) items must be delivered, our answer is at least the sum of shortest distance from \(u_1\) to \(v_1\), \(u_2\) to \(v_2\) and so on until \(u_k\) to \(v_k\). This can be found by running \(k\) times of Dijkstra’s algorithm.
- After finish delivered one item, Abu must use the shortest path to the next item pickup location in the optimum delivery path. Hence, we can construct a reduced complete graph with \(k\) node and let
dist[i][j]represent the adjacency matrix of the reduced graph. We then fill indist[i][j]with
- Case of \(-1\). We are required to output \(-1\) if it is impossible to deliver all item. The trivial one are, if there is no path from \(u_i\) to \(v_i\) then output \(-1\). The less trivial one are, if \(\text{dist}(i, j) = -1\) for any \((i, j)\) then output \(-1\). To see this, let \(\text{dist}(a, b) = -1\), this means that there is no path from \(v_a\) to \(u_b\). This also means that you have no way to go pickup item \(b\) after delivering item \(a\) (and the opposite situation too, \(a\) after \(b\)) which implies that Abu is unable to deliver all items.
- Memory limit and long long. First, we need to use long long, at worst case there are \(10^4\) cities with all roads are \(10^6\) in length, which lead to \(10^{10}\) shortest path distance if the graph is a straight line graph. Using int might lead to a Wrong Answer verdict. With our dp table of size \(2^{18} \cdot 18\) and memory to store the original graph you can notice that there is not much left from the memory limit of 64 MB. Hence, we have to be careful not to exceed the memory limit when implementing the solution.
- This TSP is a variant of the original TSP as in this problem, Abu no need to go back to the beginning after delivering his last item.
We now have a complete graph of \(k\) node, and we want to run TSP algorithm on it to find our solution. Naive TSP algorithm would get a time limit exceeded verdict as it is \(O(k!)\) and \(1 \le k \le 18\). We need a faster TSP algorithm with the help of dynamic programming.
The naive TSP algorithm explore all \(k!\) permutation search space, but there is certainly overlapping subtask. For example, \(A{-}B{-}C{-}[\text{other } k-3 \text{ items}]\) and \(B{-}A{-}C{-}[\text{other } k-3 \text{ items}]\) has overlapping subtask, and the minimum for \(C{-}[\text{other } k-3 \text{ items}]\) will always be the same. Hence, we can avoid this recomputation with dp memorization.
Let
\[\begin{align*} bitmask =& \text{ base } 2 \text{ integer with } k \text{ digits } (\therefore 0 \le bitmask < 2^k) \\ \text{remaining}(bitmask) =& \text{ }\{\text{item } i: i\text{-th digit of }bitmask\text{ is } 0 \} \\ \text{dp}(bitmask, last) =& \text{ minimum distance to deliver all item in remaining}(bitmask) \\ &\text{ and Abu is currently at position }v_{last} \end{align*}\]The above definition can be understood as, the variable \(bitmask\) is used to represent a set and if \(i\)-th bit is \(1\) represent that the \(i\)-th item had been delivered and \(\text{dp}(bitmask, last)\) is the minimum distance for Abu to further travel to deliver the remaining items given that Abu had just finish delivered the \(last\)-th item.
Then we need to have the recurrence relation and base case.
Base case:
The base case is when Abu has no more item to deliver, and thus the minimum distance to deliver the remaining item is \(0\).
\[\text{dp}(111\cdots1_2, last) = \text{dp}(2^k-1, last) = 0 \quad \text{for} \quad last = 0, 1, \ldots, k-1\]Recurrence:
After Abu had delivered his last item, Abu is at position \(v_{last}\). Abu need to choose his next destination, \(u_i\) such that \(i \in \text{remaining}(bitmask)\). Among all destination Abu can choose, he must choose the one that requires minimum travel distance. And after Abu had chosen the next item \(i\) and delivered, Abu will be at position \(v_i\) and \(i\)-th item is delivered, so we need to include \(i\)-th bit in our \(bitmask\).
\[\displaylines{ \text{dp}(bitmask, last) = \text{min}(\ \ \text{dist}(v_{last}, u_i) + \text{dp}(bitmask + 2^i, i)\ \ ) \\ \forall i \in \text{remaining}(bitmask) }\]The answer:
After the dp table is computed, we can obtain our answer at
\[\displaylines{ \text{minimum distance} = \text{min}(\ \ \text{dp}(2^i, i)\ \ ) + \sum{\text{min_dist}(u_i, v_i)} \\ \text{for } 0 \le i < k }\]It is \(\text{min}(\ \ \text{dp}(2^i, i)\ \ )\) because there is no cost on choosing which item to start deliver.
C - Eli’s Curious Mind
I would say this problem is actually quite hard because it takes time to understand the problem. At the moment I understand the problem, it seems dp-ish. So, I started to get my hands dirty on small cases and try to figure out the recurrence relation.
Note: get your hands dirty is a problem solving tactic that I learned from the book The Art and Craft of Problem Solving by Paul Zeitz. It means that try out some cases on a paper.
Solution: Dynamic Programming (Code)
The problem may seem unclear at first. But it gets better when you gets your hand dirty. Try to list out the answer for a given small \(N\) with pen and paper and repeat on more different \(N\).
Let \(T_n\) be the number of different mixtures that can be made with \(N\) chemical.
| \(N\) | mixture | \(T_n\) |
|---|---|---|
| 1 and 2 | none | 0 |
| 3 | \(\{1, 3\}\) | 1 |
| 4 | \(\{1, 3\}, \{1, 4\}, \{2, 4\}\) | 3 |
| 5 | \(\{1, 3, 5\}, \{1, 4\}, \{2, 4\}, \{2, 5\}\) | 4 |
| 6 | \(\{1, 3, 5\}, \{1, 3, 6\}, \{1, 4, 6\}, \{2, 4, 6\}, \{2, 5\}\) | 5 |
| 7 | \(\{1, 3, 5, 7\}, \{1, 3, 6\}, \{1, 4, 6\}, \{1, 4, 7\},\) \(\{2, 4, 6\}, \{2, 4, 7\}, \{2, 5, 7\}\) |
7 |
During the process, you may have observed the following:
- for a valid combination set, the gap cannot be larger or equal to \(3\). If there is such case, according to rule 2, you must include the chemical in between.
- if there is total \(N\) chemical, the last chemical in a valid mixture could only be \(N\) or \(N-1\). If the last chemical is \(N-2\) or smaller, you can always include \(N\) to make a new mixture, hence, according to rule 2, it is invalid.
Until now, for those who have some experience in competitive programming, this problem may seem dp-ish. Hence, now we should focus on finding the recurrence relation. If you can find the recurrence relation you solve the dp problem. A common strategy when dealing with such problems is to find out whether the solution for \(N\) can be built from smaller \(N\).
The key to solve this problem is actually defining \(S_n =\) number of mixture that has last chemical as \(N\) and we find \(S_n\) instead of \(T_n\). \(T_n\) can be found using \(T_n = S_n + S_{n-1}\) (because of observation 2). Now, \(S_n\) can be obtain using dp.
\[\displaylines{ S_n = S_{n-2} + S_{n-3} \quad \text{for} \quad n > 5 \\ S_1 = S_2 = 0 \\ S_3 = 1 \quad S_4 = 2 \quad S_5 = 2 }\]Why? Because, for a mixture that end with chemical \(n\), the previous chemical must be either \(n-2\) or \(n-3\). It cannot be \(n-1\) because of rule 1 and it cannot be less than \(n-3\) because of observation 1. So to make a new mixture that ends with chemical \(n\), we take the mixtures that ends with chemical \(n-2\) and \(n-3\) then add chemical \(n\) to them. Hence, we have \(S_n = S_{n-2} + S_{n-3}\).
Our base case is \(n = 1, 2, 3, 4, 5\) because, up to \(n=5\) we are able to select chemical 1 and 2 as the next-to-last chemical. This will cause problems as \(S_1 = S_2 = 0\).
D - Explorace
At some point of time during the contest, my teammates identified it as a MST problem and come to me. My reaction was like “hmm MST. Okayyy. no trick? no catch?”. After double confirming that there is no other trick in this problem, I asked my teammates to “copy and paste” the MST code from our cheatsheet and get AC (should be “read and type” but whatever).
Solution: Graph - Direct MST (Code)
This is a straightforward MST (Minimum Spanning Tree) problem. Implement a MST algorithm with either Prim’s or Kruskal’s to get AC.
E - Matrix Multiplication Calculator
I found this problem when my teammate was implementing his solution for G. This is a straightforward and easy implementation problem. Immediately after he finished coded G and get AC. I took over the PC and coded it in 10 minutes and get a speedy AC.
Solution: Ad-Hoc - Implementation (Code)
This is an Ad-Hoc implementation problem. One method to helps in implementing the solution is by defining a function multiply(int r, int c) such that multiply(r, c) returns the r-th row, c-th column of the answer matrix.
int multiply(int i , int j){
int ans = 0;
for(int k = 0; k < c1; k++){
ans += a[i][k] * b[k][j];
}
return ans;
}
After you have the function, the rest is just the problem on input and output format.
F - Sum of Sub Rectangle Areas
This is the hardest problem in the competition. I found this problem and immediately knows that the direction to solve it is to derive an \(O(1)\) closed-form equation aka formula. After some preliminary math session, I manage to obtain a \(O(N)\) solution but it is not fast enough.
Eventually I stuck at a part that are relatively simple, that is, find a \(O(1)\) equation for the sum \(1\cdot2 + 2\cdot3 + \cdots + (n-1)\cdot n\) and I am quite frustrated at it. My mathematics skill has been deteriorate since I stopped doing olympiad math actively (which is the time when I got to my university). It gets even more frustrating when I saw another team had solved the problem while I am still helpless at the sum. I was like, “noooooo, my math has lost to another team” (yes, I am proud of my mathematics). This almost cost us losing the contest.
I had tried almost all sort of way to find the \(O(1)\) equation, including trying to fit a polynomial to the function by try-and-error-ing its coefficient but none of them leads to something useful.
After we had cleared almost all the easy and medium problems, all members of our team involved in deriving the equation. And eventually one of my teammates mentions something about “it seems to has something to do with sum of squares”. Anything happens after this, is pure luck and magic.
“Sum of squares” is what helps us in this problem. I then tell him, “hmm okay, sum of squares, I remember that the formula for sum of square is \(\frac{(n)(n+1)(n+2)}{6}\)”. Then I started to play around with the equation and try plugging in \(n\) and see the correlation with the answer and “holy crap !!! this is the answer !!!”“. If this is not luck, I don’t know what is.
Note: the correct formular for sum of squares is \(\frac{(n)(n+1)(2n+1)}{6}\)
Solution: Math - Combinatorics (to obtain the equation) + Algebra (to simplify the equation) (Code)
There is a reason why this is the hardest problem. Because it is not easy to obtain the \(O(N)\) equation either. It might be harder than simplifying the equation from \(O(N)\) to \(O(1)\).
During the contest, I had drawn a very helpful diagram that helps in obtaining the equation. Let’s use some diagrams to help in deriving the equation.
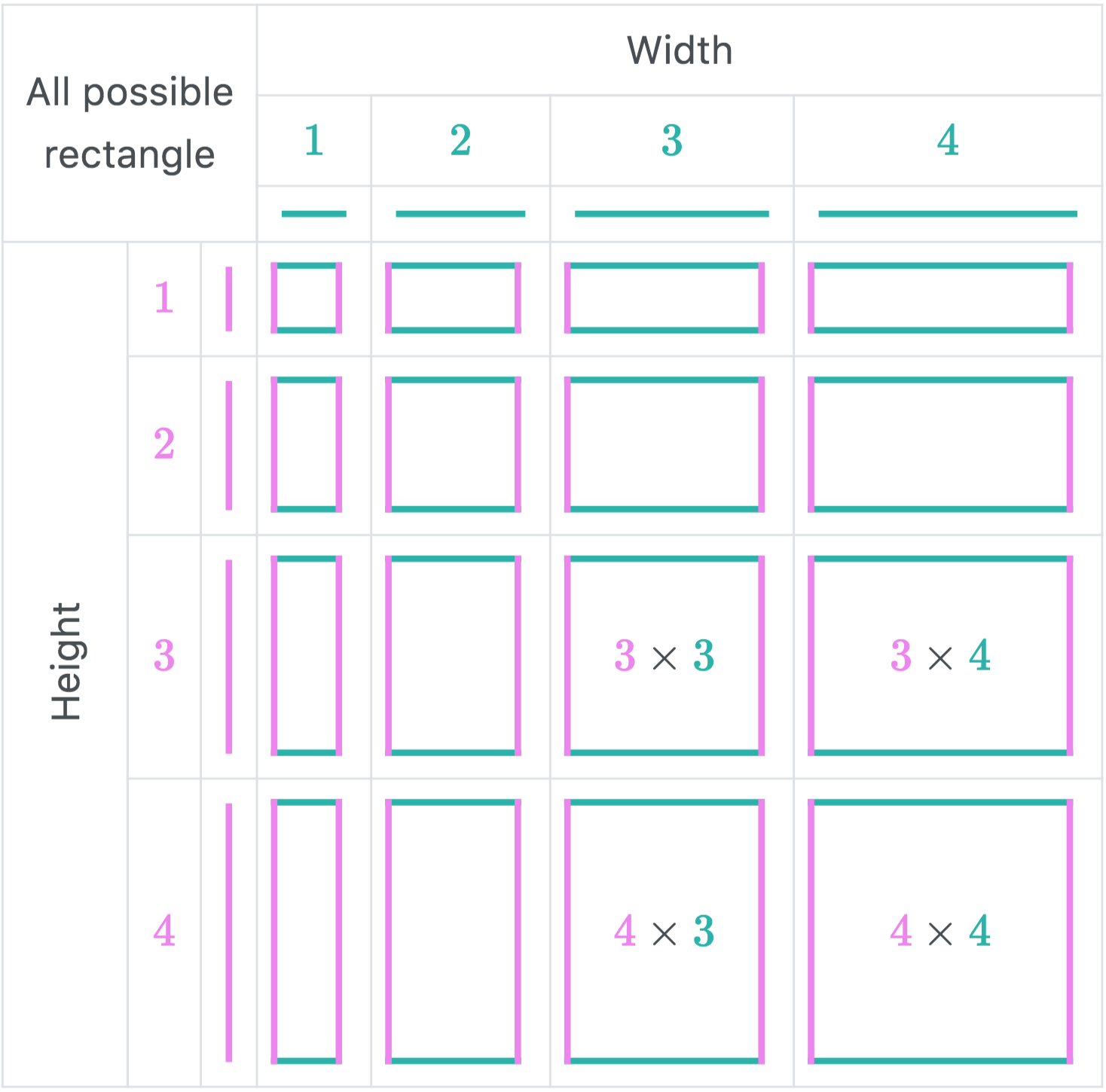
The above diagram shows that all possible subrectangles of a square of side length \(n\) can be list down in a table of size \(n \times n\). We will be using the table similar to the diagram above for the following explanation.
It is important to understand that the table cell of \(r\)-th row and \(c\)-th column represent the subrectangles of size \(r \times c\).
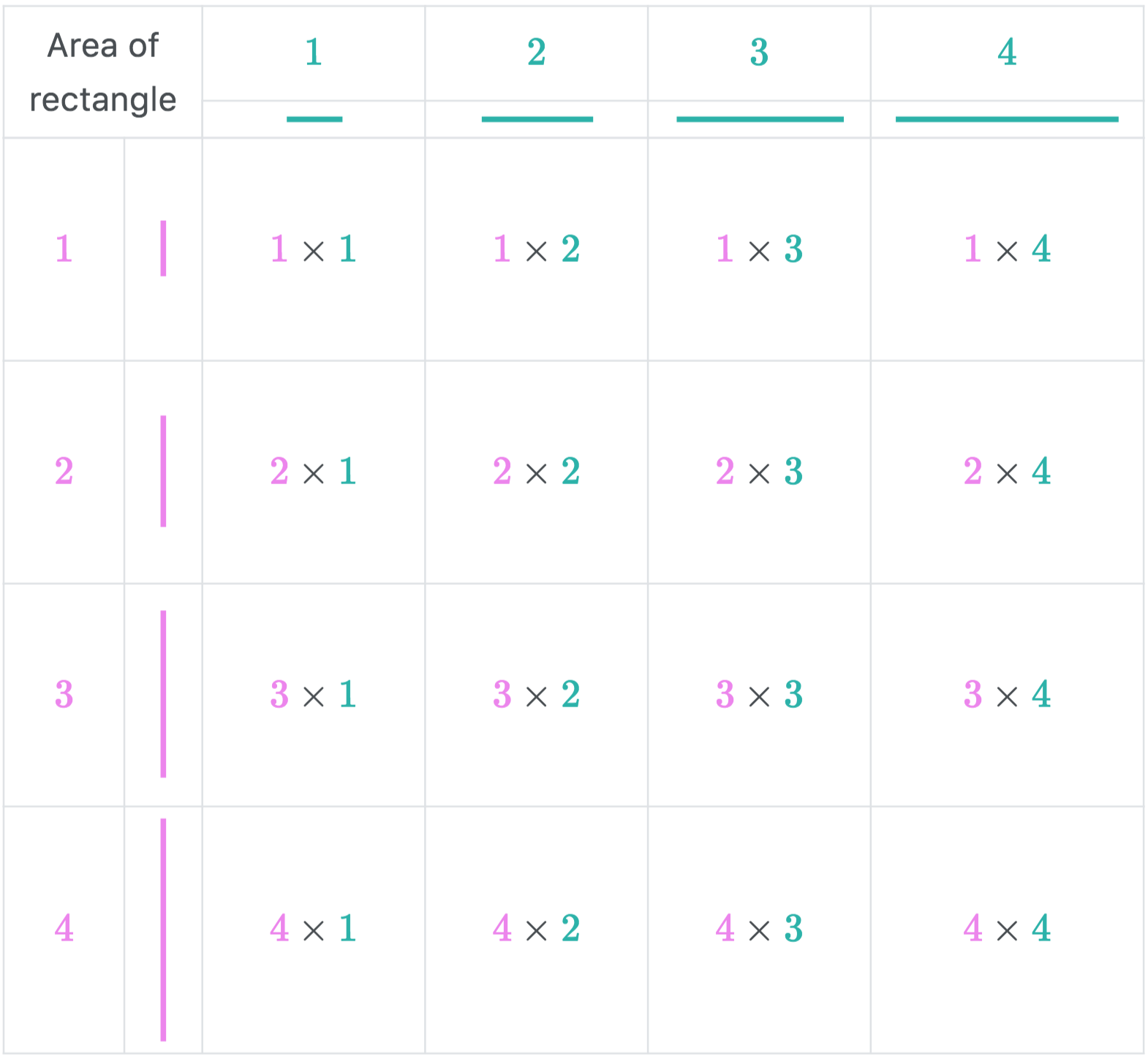
The diagram above is pretty straightforward, each table cell represent the area of the rectangle of a given size.
The above diagram computes the number of different subrectangles for every given size. We use \(n\) for the sake of generalization.
To understand the diagram, you should answer the following combinatorics problem yourself:
Given a \(n \times n\) square, how many different \(2 \times 2\) subrectangles are in the square. What about \(2 \times 3\) ?? What about \(3 \times 2\) ??
Answer: There are \((n-1)\times(n-1)\) different \(2 \times 2\) subrectangles, \((n-1)\times(n-2)\) different \(2 \times 3\) subrectangles and \((n-2)\times(n-1)\) different \(3 \times 2\) subrectangles as correspond to the diagram above.
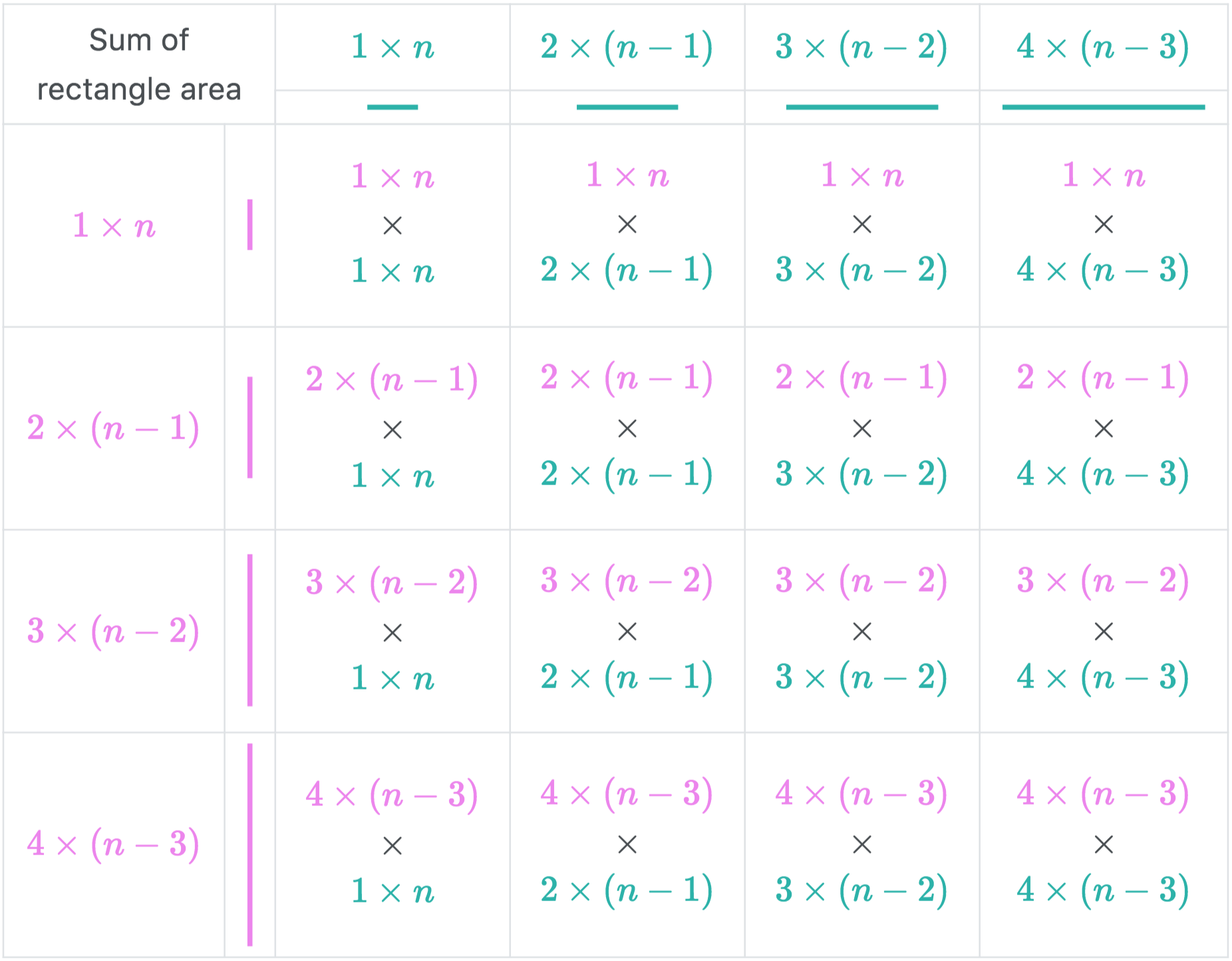
Finally, if we have the number of different rectangles of a given size and multiply that amount with their area, we will get sum of subrectangle areas of given size. The total sum is just the sum across all subrectangle of different sizes.
For example, let’s focus on subrectangle of size \(3 \times 2\). There are \((n-2)\times(n-1)\) different subrectangle of such size, and their area is \(3 \times 2\). Thus, the sum of subrectangle area of size \(3 \times 2\) is \(\left[ (n-2) \times (n-1) \right] \times \left[ 3 \times 2 \right]\). This is correspond to row \(3\) column \(2\) of the table above.
Now it is not hard to see that the answer to the problem is the sum of all terms in the table above. So, let’s add them up.
Let \(S_n\) be the sum of subrectangle area of square of side length \(n\).
\[\begin{align*}S_n &= \textcolor{violet}{\left[ 1 \times n \right] } \times \textcolor{lightseagreen}{\left[ 1 \times n \right] } + \textcolor{violet}{\left[ 1 \times n \right] } \times \textcolor{lightseagreen}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{violet}{\left[ 1 \times n \right] } \times \textcolor{lightseagreen}{\left[ n \times 1 \right]} \\ &+ \textcolor{violet}{\left[ 2 \times (n-1) \right] } \times \textcolor{lightseagreen}{\left[ 1 \times n \right] } + \textcolor{violet}{\left[ 2 \times (n-1) \right] } \times \textcolor{lightseagreen}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{violet}{\left[ 2 \times (n-1) \right] } \times \textcolor{lightseagreen}{\left[ n \times 1 \right]} \\ &+ \textcolor{violet}{\left[ 3 \times (n-2) \right] } \times \textcolor{lightseagreen}{\left[ 1 \times n \right] } + \textcolor{violet}{\left[ 3 \times (n-2) \right] } \times \textcolor{lightseagreen}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{violet}{\left[ 3 \times (n-2) \right] } \times \textcolor{lightseagreen}{\left[ n \times 1 \right]} \\ &\ \ \vdots \\ &+ \textcolor{violet}{\left[ n \times 1 \right] } \times \textcolor{lightseagreen}{\left[ 1 \times n \right] } + \textcolor{violet}{\left[ n \times 1 \right] } \times \textcolor{lightseagreen}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{violet}{\left[ n \times 1 \right] } \times \textcolor{lightseagreen}{\left[ n \times 1 \right]} \\[10px] S_n &= \textcolor{violet}{\left[ 1 \times n \right] } \ \bigl( \ \textcolor{lightseagreen}{\left[ 1 \times n \right] } + \textcolor{lightseagreen}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{lightseagreen}{\left[ n \times 1 \right]} \ \bigr) \\ &+ \textcolor{violet}{\left[ 2 \times (n-1) \right] } \ \bigl( \ \textcolor{lightseagreen}{\left[ 1 \times n \right] } + \textcolor{lightseagreen}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{lightseagreen}{\left[ n \times 1 \right]} \ \bigr) \\ &+ \textcolor{violet}{\left[ 3 \times (n-2) \right] } \ \bigl( \ \textcolor{lightseagreen}{\left[ 1 \times n \right] } + \textcolor{lightseagreen}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{lightseagreen}{\left[ n \times 1 \right]} \ \bigr) \\ &\ \ \vdots \\ &+ \textcolor{violet}{\left[ n \times 1 \right] } \ \bigl( \ \textcolor{lightseagreen}{\left[ 1 \times n \right] } + \textcolor{lightseagreen}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{lightseagreen}{\left[ n \times 1 \right]} \ \bigr) \\[10px] S_n &= \bigl( \ \textcolor{lightseagreen}{\left[ 1 \times n \right] } + \textcolor{lightseagreen}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{lightseagreen}{\left[ n \times 1 \right]} \ \bigr) \bigl( \ \textcolor{violet}{\left[ 1 \times n \right] } + \textcolor{violet}{\left[ 2 \times (n-1) \right]} + \cdots + \textcolor{violet}{\left[ n \times 1 \right]} \ \bigr) \\ &= \bigl( 1 \times n + 2 \times (n-1) + \cdots + n \times 1 \bigr)^2 \\ \end{align*}\]Now we got our \(O(n)\) equation. To simplify it to \(O(1)\) we need some algebra trick and formulas.
\[\begin{align*} S_n &= \bigl( 1 \times n + 2 \times (n-1) + \cdots + n \times 1 \bigr)^2 \\ &= \bigl( \left[ 1 \cdot n \right] + \left[ 2 \cdot (n-1) \right] + \cdots + \left[ n \cdot (n-(n-1)) \right] \bigr)^2 \\ &= \bigl( \left[ n \right] + \left[ 2n - 2(1) \right] + \left[ 3n - 3(2) \right] + \cdots + \left[ n^2 - n(n-1) \right] \bigr)^2 \\ &= \bigl( n + 2n + 3n + \cdots + n^2 - \left[ 1(2) + 2(3) + 3(4) + \cdots + (n-1)(n) \right] \bigr)^2 \\ &= \bigl( n\left( 1 + 2 + 3 + \cdots + n \right) - \left[ 1(2) + 2(3) + 3(4) + \cdots + (n-1)(n) \right] \bigr)^2 \\ &= \left( n \cdot \frac{n(n+1)}{2} - \bigl[ \ 1(2) + 2(3) + 3(4) + \cdots + (n-1)(n) \ \bigr] \right)^2 \\ \end{align*}\]Now the only problem left is to find an \(O(1)\) equation for the expression
\[\begin{equation} 1(2) + 2(3) + 3(4) + \cdots + (n-1)(n) \label{eq1} \tag{1} \end{equation}\]With some observation, we can see that
\[\begin{align*} \eqref{eq1} &= 1(1+1) + 2(2+1) + 3(3+1) + \cdots + (n-1)((n-1) + 1) \\ &= 1^2 + 1 + 2^2 + 2 + 3^2 + 3 + \cdots + (n-1)^2 + (n-1) \\ &= 1^2 + 2^2 + 3^2 + \cdots + (n-1)^2 + 1 + 2 + 3 + \cdots + (n-1) \\ &= \frac{(n-1)(n)(2(n-1)+1)}{6} + \frac{(n-1)(n)}{2} \\ &= \frac{(n-1)(n)(2n-1)}{6} + \frac{(n-1)(n)}{2} \\ &= \frac{(n-1)(n)}{2} \left( \frac{2n-1}{3} + 1 \right) \\ &= \frac{(n-1)(n)}{2} \left( \frac{2n-1 + 3}{3} \right) \\ &= \frac{(n-1)(n)(2n+2)}{6} \\ &= \frac{(n-1)(n)(n+1)}{3} \\[10px] S_n &= \left( \frac{n^2(n+1)}{2} - \frac{(n-1)(n)(n+1)}{3} \right)^2 \\ &= \left( n(n+1) \cdot \left(\frac{n}{2} - \frac{n-1}{3} \right) \right)^2 \\ &= \left( n(n+1) \cdot \left(\frac{3n - 2n + 2}{6} \right) \right)^2 \\ &= \left(\frac{n(n+1)(n+2)}{6}\right)^2 \quad (Q.E.D.) \\ \end{align*}\]G - Wak Sani Satay
I actually never understand the problem during the contest. My teammate says he knows how to do this, and I was like “okay, then thank you very much, I go read other problem”. Hence, I have nothing much to say about this problem.
Solution: Ad-Hoc - Understanding Problem (Code)
This problem can be solved by a careful reading of the problem, understanding it correctly and implementing it correctly. One trick to solve such understanding problems is to translate the problem from English to Mathematics. The translations are:
- \(1\)kg meat \(= 85\) satay
- retail price
- nasi impit \(= 0.8\) per packet
- chicken satay \(= 0.8\) per stick
- beef satay \(= 1.0\) per stick
- lamb satay \(= 1.2\) per stick
- cost
- chicken meat \(= 7.5\) per kg
- beef meat \(= 24.0\) per kg
- lamb meat \(= 32.0\) per kg
- marinate meat for satay \(= 8.0\) per kg
- nasi impit \(= 0.2\) per packet
with the information above, the net profit is trivial:
- cost per satay
- chicken \(= 7.5\;/\;85 + 8.0\;/\;85\)
- beef \(= 24.0\;/\;85 + 8.0\;/\;85\)
- lamb \(= 32.0\;/\;85 + 8.0\;/\;85\)
- net profit \(=\) retail price \(-\) cost
- chicken = \(0.8 - (7.5\;/\;85 + 8.0\;/\;85)\) per satay
- beef = \(1.0 - (24.0\;/\;85 + 8.0\;/\;85)\) per satay
- lamb = \(1.2 - (32.0\;/\;85 + 8.0\;/\;85)\) per satay
- nasi impit \(= 0.8 - 0.2 = 0.6\) per packet
Finally, with all the information above we can just take amount \(\times\) net profit to get the total net profit.
H - Stroop Effect
Another problem that I actually did not understand during the contest. My teammates solved this problem together. I think I was busy deriving F at that time.
Solution: Ad-Hoc - Understanding Problem (Code)
Another understanding problem like G but more complicated and longer problem statement. This problem require a stronger English basics and sense of logic to understand it. Same as above, we translate English to Mathematics. We get:
- You are given a sequence of 2 letter string consist of character ‘1’, ‘2’, ‘3’, ‘4’
- The sequence is a Stroop sequence if and only if all of the following condition are true:
- number of “\(xx\)” must be equal to number of “\(xy\)” where \(x \ne y\) and \(x, y \in \{1, 2, 3, 4\}\)
- for set of “\(xx\)”, number of ‘1’ = number of ‘2’ = … = number of ‘4’
- for set of “\(xy\)”, number of ‘1’ = number of ‘2’ = … = number of ‘4’
- for each “\(xy\)”, number of “\(x_1y_1\)” = number of “\(x_2y_2\)” = … = number of “\(x_4y_4\)”
- for sequence “\(a_1b_1\)”, ”\(a_2b_2\)”, ”\(a_3b_3\)”, \(\ldots\), ”\(a_nb_n\)”, \(a_i = a_{i+1} = a_{i+2}\) or \(b_i = b_{i+1} = b_{i+2}\) IS NOT ALLOWED
Now, note that we can simplify the 5 conditions above to the 4 conditions below for the ease of implementation:
- let congruent = number of “\(x_1x_1\)” = number of “\(x_2x_2\)” = …
- let incongruent = number of “\(x_1y_1\)” = number of “\(x_1y_2\)” = …
- congruent \(\times 4\) == incongruent \(\times 12\)
- for sequence “\(a_1b_1\)”, ”\(a_2b_2\)”, ”\(a_3b_3\)”, \(\ldots\), ”\(a_nb_n\)”, \(a_i = a_{i+1} = a_{i+2}\) or \(b_i = b_{i+1} = b_{i+2}\) IS NOT ALLOWED
Checking all 4 conditions above will give you an AC.
I - Super Ball
This problem was a total failure. We did not solve it during the contest. At first glance, the problem seems min cost flow to me. I have such thought because there is one min cost flow problem in previous ICPC too. Then, I started to model the graph on a paper and analyze the complexity. The graph that I modeled is super messy and contain too many nodes. We end up giving up this problem because the time is running out and it is impossible to code a bug-free solution in that time limit.
After the contest, I think about the problem again and dp seem to be able to solve the problem because it looks like a directed acyclic graph. My dp assumption was further confirmed by the problem setter.
Back to home, I coded the dp solution and pass the test data in 30 minutes and I was speechless at that moment. I failed because I “think too much”.
Solution: Dynamic Programming (Code)
It is not so trivial that it is a DAG (directed acyclic graph) but once you assume it is a DAG, you can start to see the properties of DAG in the problems.
First of all, let’s make some observation:
- the process of producing and recycling are independent to each other. Hence, they can be counted separately.
- the process of producing and recycling is exactly the same. Hence, they can be computed using the exact same algorithm. (From now on, we will only be focus on the algorithm to find the cost for producing, recycling is just producing in reverse direction)
- you must go through \(N\) factory to produce \(N\) layer. (I know you can produce \(2\) layer at the same factory but for the sake of generalization, let’s assume that this process is produce layer \(1\) then transfer to same factory with cost of \(0\) then produce layer \(2\))
The following flow graph represents our problem. The capacity of the edge in the following flow graph is all \(1\). The min cost flow of the following graph will be our answer to this problem.
However, you do not need a min cost flow algorithm to solve the problem. Since the graph above is a DAG, you can use dynamic programming to solve the problem.
Note: the following solution use \(0\)-based indexing to be consistent with my code solution
Let
\[\begin{align*}\text{dp}(l, f) =& \ \text{cost to produce layer } 0 \text{ to layer } l \textbf{ and } \\ & \ \text{the ball is currently at factory } f \\ \text{cost}(l, f) =& \ \text{cost to produce layer $l$ at factory $f$} \\ \text{cost}(l, f) =& \ \infty, \quad \text{if factory $f$ is unable to produce layer $l$} \\ \text{dist}(f_1, f_2) =& \ \text{cost to transfer the ball from factory $f_1$ to $f_2$} \end{align*}\]Base case:
\[\text{dp}(0, f) = \text{cost}(0, f) \quad \text{for} \quad 0 \le f < F\]Recurrence:
A bit similar to B, after the ball is at factory \(f\), the ball has to choose its next destination to produce its next layer. The ball can choose any of the factories as long as the factory is able to produce its next layer.
\[\displaylines{ \text{dp}(l, f) = \text{min}(\ \ \text{dist}(i, f) + \text{cost}(l, f)+ \text{dp}(l-1, i)\ \ ) \\ \text{for} \quad 0 \le i, f < F, \ \ 1 \le l < N }\]The answer:
After the dp table is computed, we can obtain our answer at
\[\text{minimum cost} = \text{min}(\ \ \text{dp}(N-1, f)\ \ ) \quad \text{for} \quad 0 \le f < F\]J - Virus Outbreak
Before the contest start, I was tasked to read and understand the last 3 problems (H, I, J). When the contest starts, I started with H, and I was like “hmm, lengthy statement, I probably should try with the next one”. Then, I continue to I and it was the same !! I continue to skip until J and finally found a shorter statement. After understands the problem ask us to identify the sequence, I list down the sequence into a table with their known corresponding value. \(1\), \(3\) and \(8\) immediately caught my attention and “It is Fibonacci !!!”. Also, I noticed that you probably need some big integer. Hence, I quickly grab the PC, coded a python solution and get the first AC in the contest at \(6\)-th minutes.
Solution: Identify the Pattern - Fibonacci (Code)
For those who are familiar with Fibonacci sequence, the number \(3\) and \(8\), should probably give you an alert that it is a Fibonacci. For those who are not familiar with the Fibonacci sequence, this problem might be hard.